基于网格的聚类方法——Wave cluster小波聚类

文中使用的代码下载：https://github.com/BaiHLiu/WaveCluster

网格聚类方法概述

引言

聚类算法是一种无监督分类算法。算法很多，包括基于划分的聚类算法（如：kmeans），基于层次的聚类算法（如：BIRCH），基于密度的聚类算法（如：DBScan），基于网格的聚类算法等等。

基于划分和层次聚类方法都无法发现非凸面形状的簇，真正能有效发现任意形状簇的算法是基于密度的算法，但基于密度的算法一般时间复杂度较高，1996年到2000年间，研究数据挖掘的学者们提出了大量基于网格的聚类算法，网格方法可以有效减少算法的计算复杂度，且同样对密度参数敏感。

一句话总结一下几种聚类方法的核心思想：

• 基于划分：类内的点足够近、类间的点足够远。我们不断更换聚类中心，直到聚类中心稳定，即为最终的结果。
• 基于密度：先发现密度较高的点，然后将相近的高密度点逐步连成一片，进而形成簇。
• 基于网格：将数据空间划分为一个个网格，将数据按照一定的规则映射到网格单元(cell)中，然后计算每个单元的密度。根据预先设定的阈值判断出每个网格单元是否为高密度单元，由临近的高密度单元组成一个类。

基本步骤

基于网格的聚类方法使用一种多分辨率的网格数据结构，它将对象空间量化成有限数目的单元（cell），这些单元形成了网格结构，所有聚类操作在该结构上进行。

分辨率

总的来说，不同的分辨率，决定了要获得更概括性还是更细节性的信息。

不同的算法有不同的网格划分方法，并对网格数据结构进行了不同的处理，但核心步骤是相同的：

1. 划分网格
2. 使用网格单元内数据的统计信息对数据进行压缩表达
3. 基于这些信息判断高密度网格单元
4. 将相连的高密度网格单元识别为簇

统计信息：例如均值，最大值和最小值

一些网格聚类方法举例

Statistical Information Grid(STING)算法

核心思想

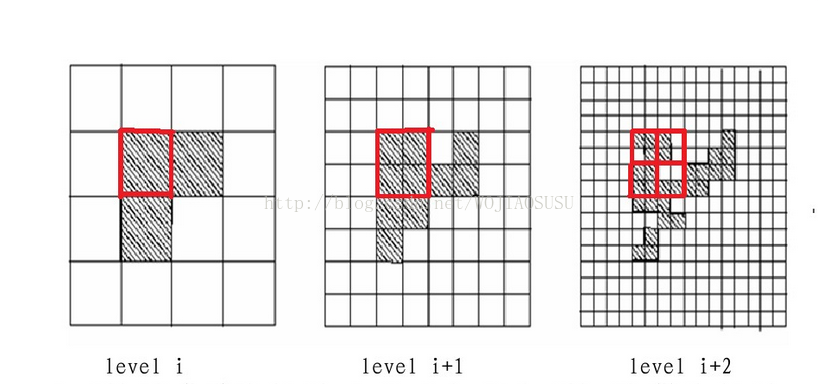
首先我们先划分一些层次，实际上这里的每个层次对应的是样本的一个分辨率。

每个高层的cell在其下一层中被对应得划分成多个cell，每个cell都计算出它的统计信息，被作为统计参数预先计算和存储。

利用这样的结构，我们很容易进行查询，从上到下开始，根据cell的统计信息计算query在每个cell的置信区间，找出最大的那个cell，然后到下一层，依次直至到最底层。这样的好处是，我们不用计算所有的样本，算法每进一层都会抛弃不相关的样本，所需的计算量会越来越少，那么速度就会很快。

常用的统计参数

• count 网格中对象数目
• mean网格中所有值的平均值
• stdev网格中属性值的标准偏差
• min 网格中属性值的最小值
• max 网格中属性值的最大值
• distribution 网格中属性值符合的分布类型。（eg：正态分布, 均匀分布）

STING算法查询时步骤：（已经计算好预先的参数）

（1） 从一个层次开始

（2） 对于这一个层次的每个单元格，我们计算查询相关的属性值。

（3） 从计算的属性值以及约束条件下，我们将每一个单元格标记成相关或者不想关。(不相关的单元格不再考虑，下一个较低层的处理就只检查剩余的相关单元)

（4） 如果这一层是底层，那么转（6），否则转（5）

（5） 我们由层次结构转到下一层，依照步骤（2）进行

（6） 查询结果得到满足，转到步骤8，否则（7）

（7） 恢复数据到相关的单元格进一步处理以得到满意的结果，转到步骤（8）

（8） 停止。

粒度趋向于0（即朝向非常底层的数据），则聚类结果趋向于DBSCAN聚类结果。

与基于密度聚类的关系：如果网格的粒度趋向于0（即朝向非常底层的数据，也就是分辨率非常高），则聚类结果趋向于DBSCAN聚类结果。

优点：

• 基于网格的计算是独立于查询的，因为存储在每个单元的统计信息提供了单元中数据汇总信息，不依赖于查询。

• 网格结构有利于增量更新和并行处理。

  增量更新：算法每进一层都会抛弃不相关的样本，不需要全部更新。

  并行处理：各个网格之间没什么联系，各自单独计算参数即可。

• 效率高。STING扫描数据库一次计算单元的统计信息，因此产生聚类的时间复杂度为O(n)，在层次结构建立之后，查询处理时间为）O(g),其中g为最底层网格单元的数目，通常远远小于n。

缺点：

• 没有斜的分界线，簇边界只有水平和竖直。
• 由于多分辨率机制，聚类质量取决于网格结构的最底层的粒度。如果最底层的粒度很细，则处理的代价会显著增加。然而如果粒度太粗，聚类质量难以得到保证。

CLIQUE算法（子空间聚类算法）

CLIQUE算法是基于网格的空间聚类算法，但它同时也非常好的结合了基于密度的聚类算法，因此既能够发现任意形状的簇，又可以像基于网格的算法一样处理较大的多维数据。

核心思想：密集网格合并

首先扫描所有网格。当发现第一个密集网格时，便以该网格开始扩展，扩展原则是：若一个网格与已知密集区域内的网格邻接并且其其自身也是密集的，则将该网格加入到该密集区域中，直到不再有这样的网格被发现为止。再继续扫描网格并重复上述过程，直到所有网格被遍历。

算法流程

总结就是：首先判断某个网格是不是密集网格，如果是密集网格。那么对其相邻的网格进行遍历，看是否是密集网格，如果是的话，那么属于同一个簇。

优点：

• 尽管潜在的网格单元数量可能很高，但是只需要为非空单元创建网格。
• 将每个对象指派到一个单元并计算每个单元的密度的时间复杂度为O(m)，整个聚类过程是非常高效的。

缺点：

• 像大多数基于密度的聚类算法一样，基于网格的聚类非常依赖于密度阈值的选择。

  （太高，簇可能丢失。太低，本应分开的簇可能被合并）

• 随着维度的增加，网格单元个数迅速增加（指数增长）。即对于高维数据，聚类效果较差。

Wave Cluster

Wave Cluster称为小波聚类，是一种基于网格的快速聚类方法，常用于包含大量离群值的多维大规模数据。

主要思想

是把多维数据看作一个多维信号来处理。它首先将数据空间划分成网格结构，然后通过小波变换将数据空间变换成频域空间，在频域空间通过与一个核函数作卷积后，数据的自然聚类属性就显现出来。由于小波变换的多分辨率特性，高分辨率可以获得细节的信息，低分辨率可以获得轮廓信息。

前置知识：离散小波变换（DWT）

离散小波变换是对基本小波的尺度和平移进行离散化。在图像处理中，常采用二进小波作为小波变换函数，即使用2的整数次幂进行划分。

小波变换概念

首先来回顾一下傅立叶变换。

傅立叶变换是一种线性积分变换，用于函数（应用上称作“信号”）在时域和频域之间的变换。作用是将函数分解为不同特征的正弦函数的和。

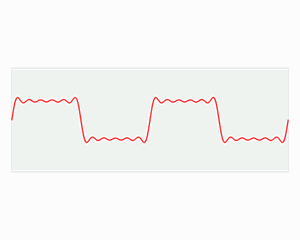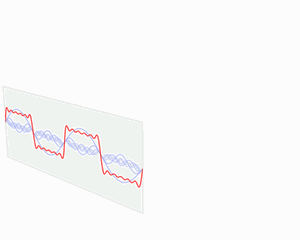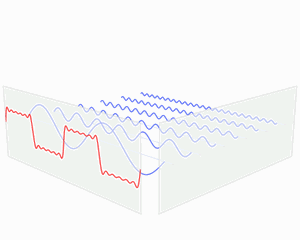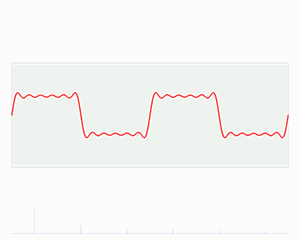
简单来说：所有的波都可以用很多个正弦波叠加表示。例子：拟合方波。

小波变换跟傅立叶变换一样能同时分析时间和频率，但是小波变换在高频时时间分辨率较好，在低频时则是频率分辨率较好。

输入输出均为连续函数称为连续小波变换；输出输出均为离散值称为离散小波变换，离散小波变换常用于信号编码。

图像压缩

对于很多信号来说，其低频分量常常蕴藏在信号的基本特征，而高频信号只是给出了信号的细节信息，如图像信号的边缘轮廓信息。

DWT例子

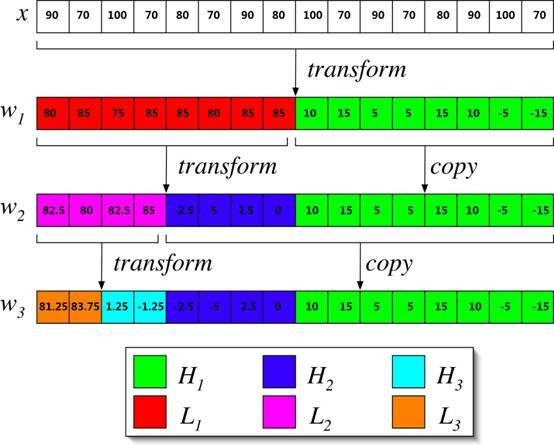
x0,x1,x2,x3=90,70,100,70

为了达到压缩效果，取 (x0+x1)/2　 (x0-x1)/2 来代表新的x0,x1

90,70 表示为 80,10　80即平均数（频率），10是小范围波动数（振幅）

同理100,70表示为85,15

80和85是局部的平均值，反映的是频率，叫做低频部分（Low-Pass）

10和15是小范围波动的幅度，叫做高频部分（High-Pass）

即90,70,100,70经过一次小波变换，可以表示为80,85,10,15，低频部分在前(L)，高频部分在后(H)

对下面的序列进行三次小波变换：

基本原理

WaveCluster算法的核心思想是将数据空间划分为网格后，对此网格数据结构进行小波变换，然后将变换后的空间中的高密度区域识别为簇。基于数据点数目大于网格单元数目（N≥K）的假设，WaveCluster的时间复杂度为O(N)，其中N为数据集内数据点数目，K为网格内的网格单元数目。

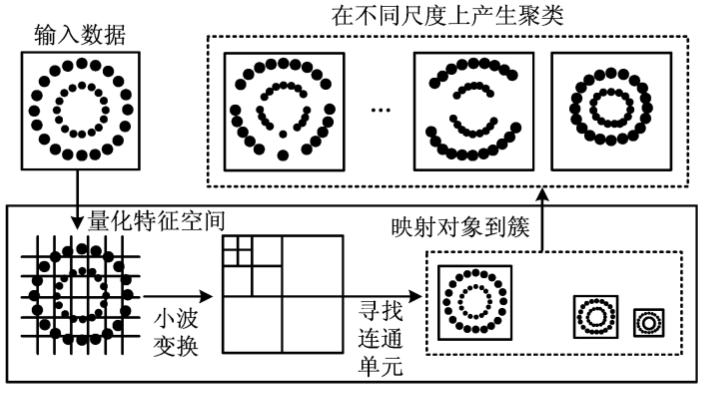
WaveCluster算法需要两个参数：

• 网格的尺寸——确定空间网格划分
• 密度阈值——网格中对象数量大于等于该阈值表示该网格为稠密网格

算法流程

1. 将原始空间离散化为网状空间，并把原始数据放入对应单元格，形成新的特征空间

   

2. 对特征空间进行小波转换，即用小波变换对原始数据进行压缩

   1. 对每行进行小波变换，得到

      

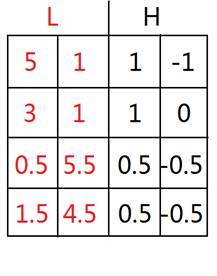
   2. 再对每列进行小波变换，得到

   

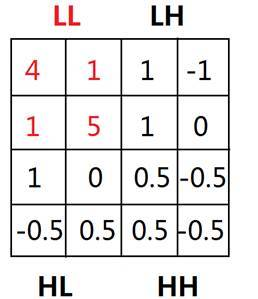
3. 找出小波转换后的LL空间中密度大于阈值（这里取3）的网格，将其标记为稠密

   

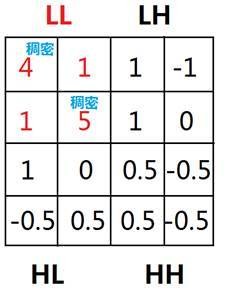
4. 对于密度相连的网格作为一个簇，打上其所在簇序号的标签

   

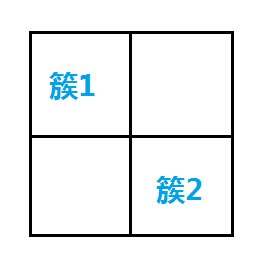
5. 建立转换前后单元格的映射表，簇标签映射到原图

   

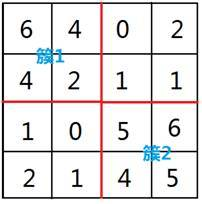
6. 把原始数据映射到各自的簇上

   

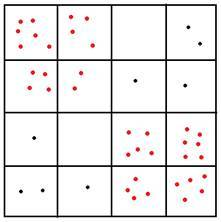
参数调整对结果的影响

由上面的分析可知，小波聚类可以调整的参数有：

• 网格的疏密（有些文章中称为尺度，scale或者level）
• 密度阈值

结果评估分析

nmi（标准化互信息）

信息增益 IG(Y|X)：衡量了知道X的情况下，对Y的不确定性减少了多少

互信息I(X;Y)：度量X和Y共享的信息，度量这两个其中知道了一个，对另一个不确定度减少的程度

二者在数值上完全相同。

理论上，互信息的值越大越好，可是其取值范围是没有上边界的。为了更好的比较不同聚类结果，提出了标准化互信息的概念，将互信息的值归一化到0和1之间，这样就可以在不同数据集之间进行比较了。标准化互信息的值越接近1，聚类效果越好。

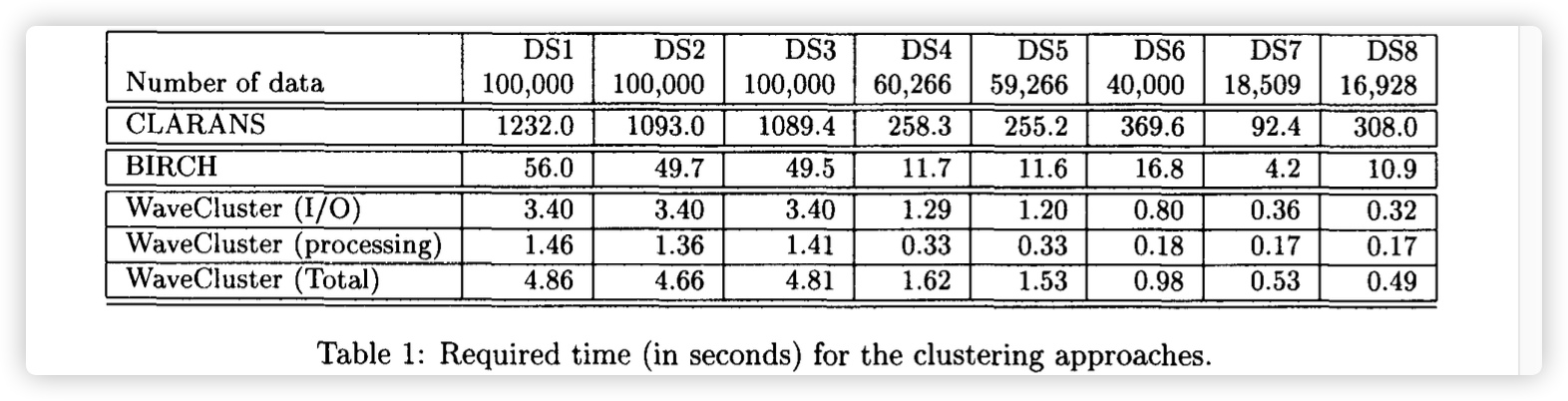
原论文上给的指标：

主要优点

• **对维度较低的情况，算法复杂度达到O(n)**，适用于巨量数据集
• 识别任意形状
• 多分辨率，能根据用户指定的scale找到任意复杂结构的聚类
• 抗噪性能良好

缺点

• 参数敏感，聚类结果非常依赖密度阈值和网格大小的选择

  阈值太高，簇可能丢失；阈值太低，本应该被分开的可能被合并

• 随着维度增加，网格单元指数增长

  即对于高维数据，聚类效果往往较差，而且时间很久

改进算法

双网格校正算法

[1]刘晓波,邵伟芹,张明明,左红艳.基于双网格校正小波聚类的转子故障诊断[J].计算机集成制造系统,2017,23(09):1883-1890.DOI:10.13196/j.cims.2017.09.007.

问题缘由：

• 网格最佳量化并没有恰当的准则，因而这种方式没有预先目的地，只能盲目寻找，直到找到结果为止。
• 同时，用一种尺寸对空间进行均匀网格量化，得到由体积大小相等的网格单元，但由于空间数据对象的分布往往不均匀，仅用一种尺寸均匀量化将掩盖住网格单元内部数据对象分布不均的事实，从而降低聚类的精度。

解决方案：应用两种尺寸对空间进行量化，并应用校正算法校正聚类结果，以提高聚类精度。

体会：降低了网格划分和网格密度阈值对聚类质量的影响；将网格划分的规模由盲目式变为启发式。

并行小波算法

Yıldırım A A, Özdoğan C. Parallel WaveCluster: A linear scaling parallel clustering algorithm implementation with application to very large datasets[J]. Journal of Parallel and Distributed Computing, 2011, 71(7): 955-962.

通过使用不同尺度级别的小波变换，在并行处理的条件下扩展了聚类速度和规模。

基于峰值网格改进的小波聚类算法

[1]龙超奇,蒋瑜,谢雨.基于峰值网格改进的小波聚类算法[J].计算机应用,2021,41(04):1122-1127.

问题缘由：小波聚类算法对经小波变换后的网格数值并没有很好地运用起来，仅通过密度阈值对其进行了分割处理。

解决方案：改进一下连通区域的判断方法，引入“峰值网格”的概念。

在同样低网格尺度下，该方法利用高密度区域的网格，能够更快地根据聚类中心寻找连通区域，同时还能分割处理较低网格划分尺度下不同的簇类，所取得的聚类结果更好。

总结

网格聚类算法是一种同样对密度参数敏感的聚类算法，可以有效减少算法的计算复杂度。基于网格的数据空间表示，使得它具有多分辨率特性，但同时效果也对网格尺度相当敏感。

Wave Cluster首先网格结构来汇总数据，然后采用一种小波变换来变换原特征空间，在变换后的空间中找到密集区域。小波变换的聚类速度很快，计算复杂度为O(n)。

应用场景

paper